On Some Inequalities Involving Harmonic Mean and Moments
Abstract:
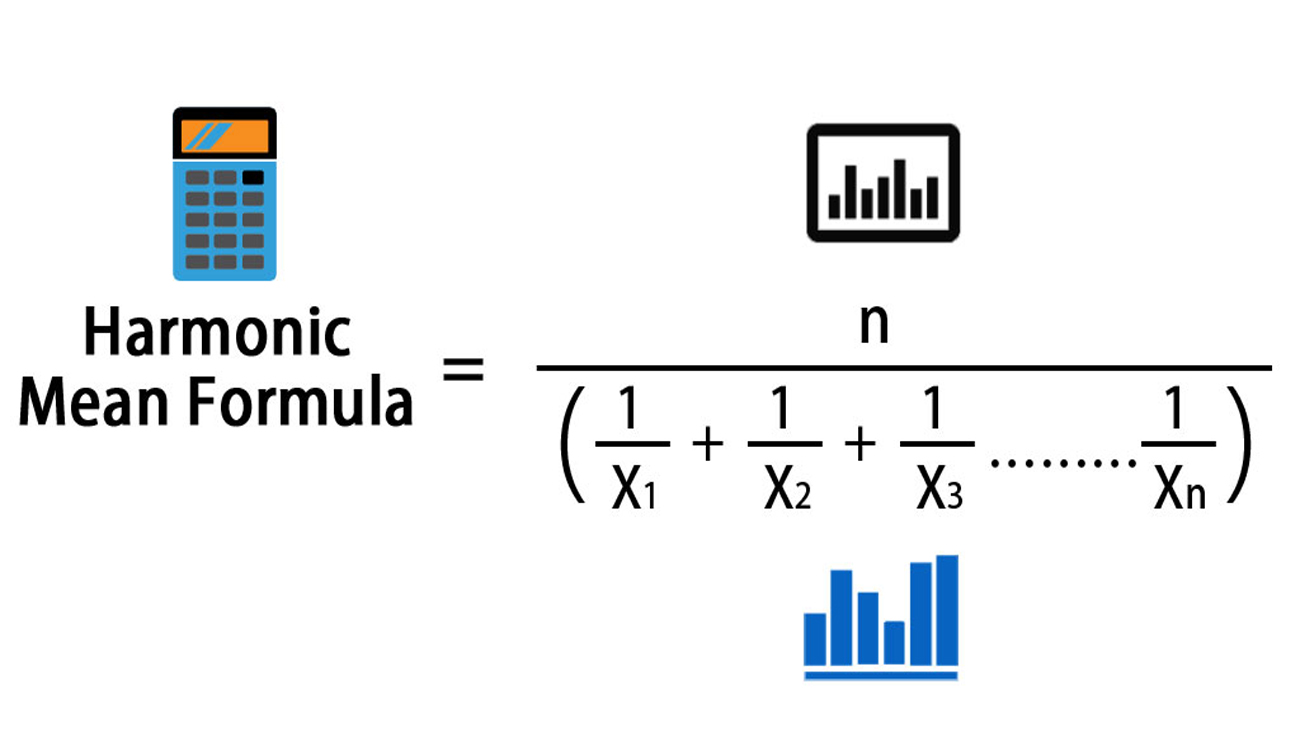
We derive bounds on the second order moment of a random variable in terms of its arithmetic and harmonic means. Both discrete and continuous cases are considered and it is shown that the present bounds provide refinements of the bounds which exist in literature. As an application we obtain a lower bound for the spread of a positive definite matrix A in terms of traces of A, A-1 and A2. Our results compare favourably with those obtained by Wolkowicz and Styan (Bounds for eigenvalues using traces, Lin. Alg. Appl. 29, 471-506, 1980).
Author(s):
DOI:
Keywords:
References:
Kantorovich, L.V., Functional analysis and applied mathematics [in Russian],Uspekki Matematicheskikh Nauk 3, 89–185, (1948).
Goldman, A. J., A generalization of Rennie’s inequality J. Res. Nat. Bur.Standards Sect. B, 68 B, 59–63 (1964).
Sharma, R., Some more inequalities for arithmetic mean, harmonic mean and variance, Math. Inequal. Appl., 2, 109–114, (2008).
Krasnosel’skii, M. A. and Kreïn, S. G., An iteration process with minimal residuals [in Russian], Mat. Sbornik N.S. 31 (73), 315–334, (1952).
Merikoski, J.K., On the Trace and Sum of elements of a Matrix, Linear Algebra and Its Applications, 60: 177–185, (1984).
Wolkowicz, H. and Styan, P.H., Bounds for Eigenvalues Using Traces, Linear Algebra and Its Applications, 29: 471–506, (1980).