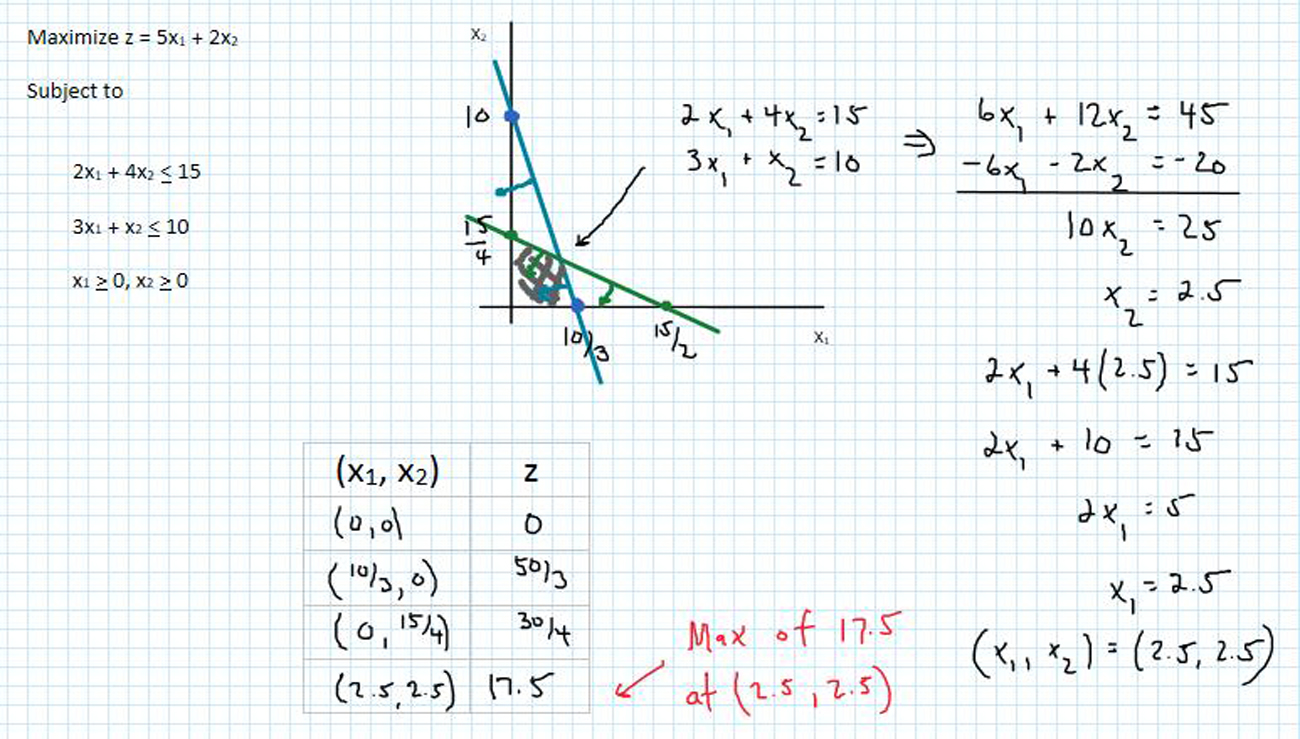
Graphical Solution and Busy Period Analysis of a Queueing Model with Feedback and Reneging
Abstract:
In the present paper, a busy period of feedback queueing model is studied. The busy period is, to begin with, the arrival of the customer to an idle system and to an end when the system next becomes idle. The customers arrive according to the Poisson process and are served by a single server according to an exponential distribution. Sometimes the customers get impatience and leave the queue without getting service with a fixed probability. The probability generating a function of a busy period by using Laplace transformation and the graphical solution of the problem is obtained. Few interesting cases are also derived to match our results with earlier published work.
Author(s):
DOI:
Keywords:
References:
A Avignon G. R. and Disney R. L., INFOR, 14, 71-85(1976).
A Ayyappan G. and Shyamala S., Malaya Journal of Matematik, 2(1), 68–76(2013).
B Bertsimas D. J., Keilson J., Nakazato D. and Zhang H., Appl. Prob., 28, 873-885(1991). http://dx.doi.org/10.2307/3214690
Choudhury G. and Paul M., Information and Management Sciences, 16 (1), 773-784(2005).
Kumari N. and Garg P .C., Int. J. Agricult. Stat. Sci., 3(2), 471-480(2007).
Perry D. and Asumssen S., Queue Syst. Theory Appl., 19, 105-130(1995). http://dx.doi.org/10.1007/BF01148942
Perry D., Stadje W., and Zacks S., Oper. Res. Letters, 27, 163-174(2000). http://dx.doi.org/10.1016/S0167-6377(00)00029-8
Sharma R. K. and Sharma S. K., American Journal of Operational Research, 2(1), 1-5(2012b). http://dx.doi.org/10.4236/ajor.2012.21001
Singh S. and Singh M., International Journal of Scientific & Engineering Research, 3(10), 1-5(2012). http://dx.doi.org/10.15373/22778179/OCT2013/59
Thangaraj V. and Vanitha S., International Journal of Pure and Applied Mathematics, 53(1), 131-151(2007).
Thangaraj V. And Vanitha S., International Mathematical Forum, 5(1), 15 – 33(2010).

