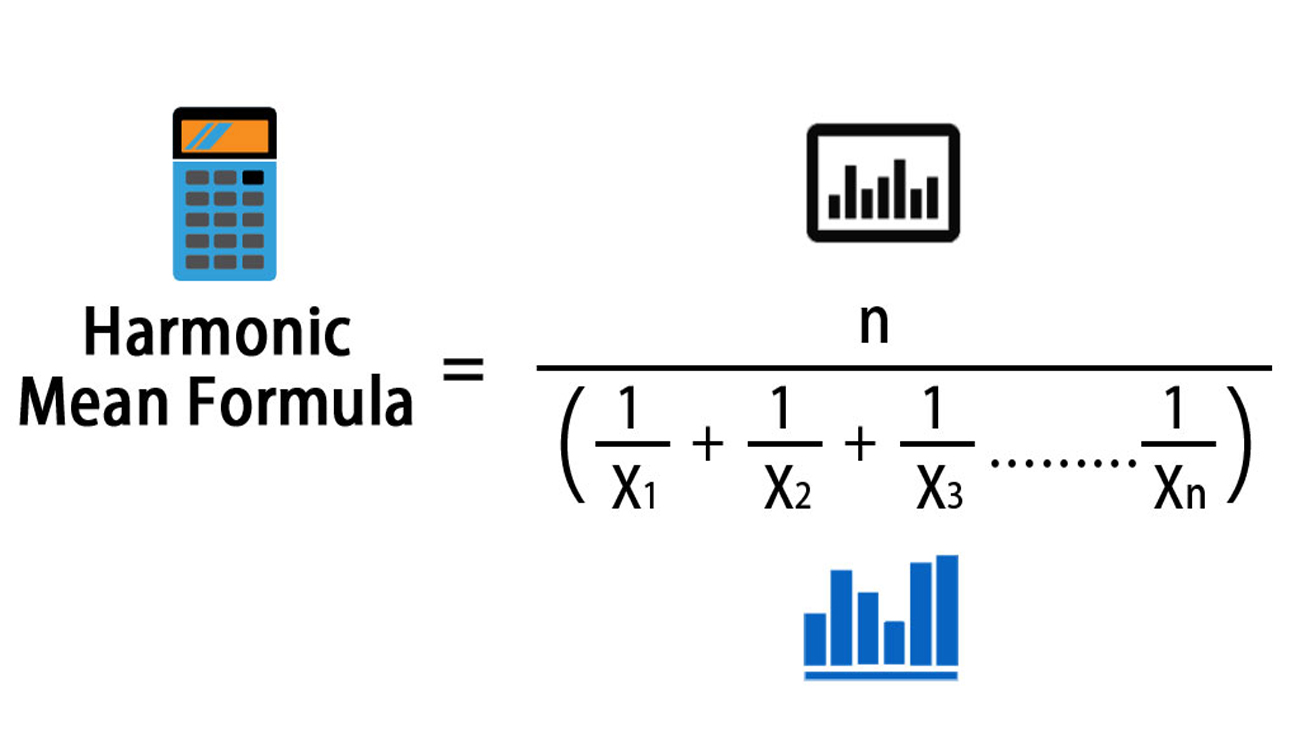
Some Elementary Inequalities Between Mean and Standard Deviation
Abstract:
Some inequalities for the mean and standard deviation of continuous probability distributions are presented here in this paper and their geometrical significance has also been discussed. It has been shown that the inequalities obtained in this paper are better than the inequalities discussed by J. Muilwijk[6].
Author(s):
DOI:
Keywords:
References:
Barnett N.S. and Drogomir S. S. Some Elementary Inequalities for the Expectation and Variance of a Random Variable whose pdf is defined on a finite interval. RGMIA Res. Rep. Coll, 2(7), Art(1), (1999).
Barnett N.S., Cerone P., Drogomir S. S. and Roumeliotis J.. Some Inequalities for the Expectation and Variance of a Random Variate whose pdf is n-times differentiable. JIPAM, Vol. 1(2), Art(21) (2000).
Bhatia, R., Davis, C.. A Better Bound on the Variance. Amer. Math. Monthly, 107, 353-357(2000). http://dx.doi.org/10.2307/2589180
Kapur J.N. and Anju Rani. Testing the Consistency of given values of a set of Moments of Probability Distribution. J. Bihar Math. Soc. 16,51- 63(1995).
Manju Shri Dutta, Ph.D. Thesis, On the Moment Values of Statistical Distribution, H.P. University, July, (2001).
Muilwijk, J.. Note on a Theorem of M.N. Murthy and V.K. Sethi. Sankhya, Ser B, 28, 183 (1966).
Sharma S.R. and Sharma R.. On Inequalities Involving Moments of Discrete Uniform Distributions. Mathematical Journal of Interdisciplinary Sciences(MJIS), Vol. 1(1),45-56(2012). http://dx.doi.org/10.15415/mjis.2012.11003
Neuman Edward, On Some Means Derived From The Schwab–Borchardt Mean II Journal of Mathematical Inequalities Volume 8, Number 2, 359–368, (2014).